본문
170818(금) - 알고리즘 for Java (AVL Tree)
알고리즘 for Java (AVL Tree)
AVL (Adelson-Velskii Lendis) Tree
· HB(1)
· 임의의 노드 n의 left sub tree와 right sub tree 높이가 최대 1
· 이진트리
- 최소 / 최대 노드 개수
· 최소
N(h) = N(h - 1) + N(h - 2) + 1
· 최대
N(h) = N(h - 1) + N(h - 1) + 1
· n개의 노드를 가진 AVL tree의 높이는 O(logn)
· AVL tree 선언
- BST와 유사하지만 높이가 추가
class AVLTreeNode<T>(var data: T) {
var left: Node<T>? = null
var right: Node<T>? = null
var height: Int? = null
}
· AVL tree height
// O(1)
fun height(root: Node<T>): Int {
return if (root == null) -1 else root.height
}
· 회전
- 삽입 / 삭제시 AVL의 속성을 유지하려면 트리를 수정해야 한다.
- single rotation & double rotation 사용
- sub tree의 높이를 증, 감 시키는 방식
· 관찰
- 삽입 / 삭제 연산 이후 이벤트가 발생한 노드부터 root까지의 sub tree만 변경 되었다.
- 따라서 회복시 해당 노드부터 root까지만 회복시키면 된다.
- 위반인 첫번째 node부터 찾아 수정
· 위반의 종류
1. left child의 left sub tree에 node insert
2. left child의 right sub tree에 node insert
3. right child의 left sub tree에 node insert
4. right child의 right sub tree에 node insert
- 1, 4는 대칭이며 single rotation으로 쉽게 해결 가능
- 2, 3도 대칭이며 double rotation으로 해결된다.
· Single rotation
- 책에 잘못된 정보가 기입되어 있다. L, R rotation을 서로 반대로 설명. 너무하네 진짜-_- 코드는 맞냐
- Right Rotation
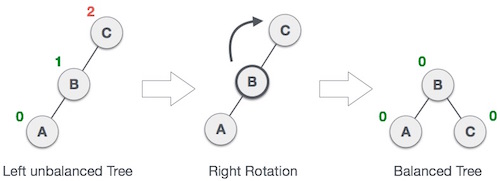
// O(1)
fun singleRightRotation(root: Node<T>): Node<T>? {
val leftNode = root.left
root.left = leftNode.right
leftNode.right = root
root.height = Math.max(treeHeight(root.left), treeHeight(root.right)) + 1
leftNode.height = Math.max(treeHeight(leftNode.left), root.height) + 1
// new root node
return leftNode
}
- Left rotation
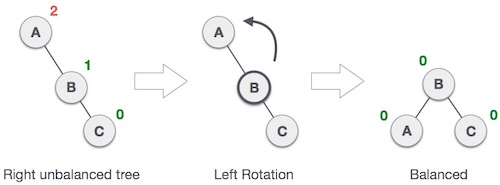
// O(1)
fun singleLeftRotation(root: Node<T>): Node<T>? {
val rightNode = root.right
root.right = rightNode.left
rightNode.left = root
root.height = Math.max(treeHeight(root.left), treeHeight(root.right)) + 1
rightNode.height = Math.max(root.height, treeHeight(rightNode.right)) + 1
// new root node
return rightNode
}
L, R 에서 height 구하는 연산에 +1을 해주는 이유는?
->
ㆍDouble rotation
- LR rotation
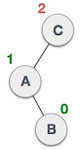
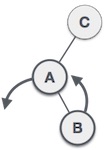
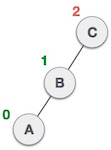
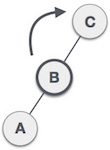
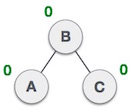
fun rotateDoubleLR(root: Node<T>): Node<T> {
root.left = rotateSingleLeft(root)
return rotateSingleRight(root)
}
- RL rotation
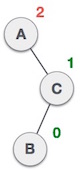
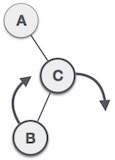
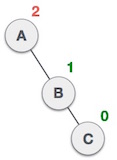
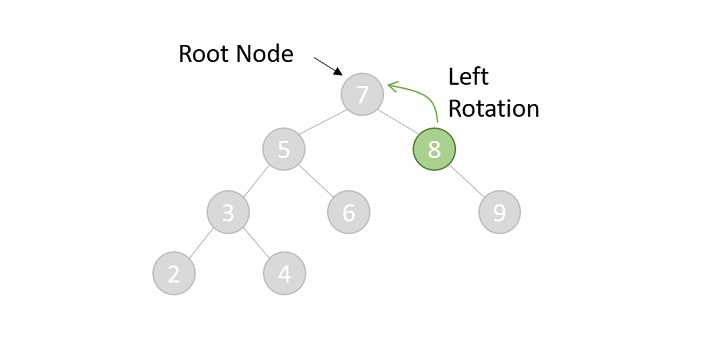

fun rotateDoubleRL(root: Node<T>): Node<T> {
root.right = rotateSingleRight(root)
return rotateSingleLeft(root)
}
ㆍAVL tree node Insert
- BST node 삽입과 매우 유사
- 높이 불균형이 발생했는지만 추가 검사
// O(n)
fun insert(root: Node<T>, parent: Node<T>, data: Int): Node<T>? {
if (root == null) {
root = Node<T>
root.data = data
root.height = 0
root.left = null
root.right = null
} else if (data < root.data) {
root.left = insert(root.left, root, data)
if (Math.abs(height(root.left) - height(root.right)) > 1) {
root = if (data < root.left.data) rotateSingleLeft(root) else rotateDoubleLR(root)
}
} else if (data > root.data) {
root.right = insert(root.right, root, data)
if (Math.abs(height(root.right) - height(root.left)) > 1) {
root = if (data > root.right.data) rotateSingleRight(root) else rotateDoubleRL(root)
}
} else {
// data가 이미 tree안에 존재한다면 아무것도 안한다.
}
root.height = Math.max(height(root.left), height(root.right)) + 1
return root
}
'Architecture > 자료구조 및 알고리즘' 카테고리의 다른 글
| 170816(수) - 알고리즘 for Java (BBST) (0) | 2017.08.16 |
|---|---|
| 170810(목) - 알고리즘 for Java (BST) (0) | 2017.08.10 |
| 170808(화) - 알고리즘 for Java (Tree) (0) | 2017.08.08 |
| 170627(화) - Stanford Engineering's Algorithms (Divide & Conquer Algorithms) (0) | 2017.06.27 |
| 170620(화) - Stanford Engineering's Algorithms (Asymptotic Analysis) (0) | 2017.06.13 |

댓글